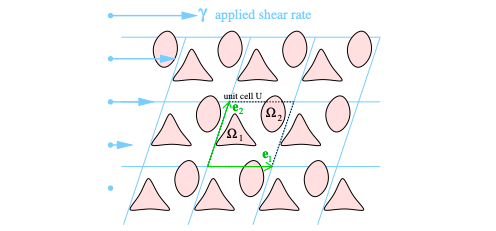
With rheology applications in mind, we present a fast solver for the time-dependent effective viscosity of an infinite lattice containing one or more neutrally buoyant smooth rigid particles per unit cell, in a two-dimensional Stokes fluid with given shear rate. At each time, the mobility problem is reformulated as a 2nd-kind boundary integral equation, then discretized to spectral accuracy by the Nystrom method and solved iteratively, giving typically 10 digits of accuracy. Its solution controls the evolution of particle locations and angles in a first-order system of ordinary differential equations. The formulation is placed on a rigorous footing by defining a generalized periodic Green’s function for the skew lattice. Numerically, the periodized integral operator is split into a near image sum|applied in linear time via the fast multipole method|plus a correction field solved cheaply via proxy Stokeslets. We use barycentric quadratures to evaluate particle interactions and velocity fields accurately, even at distances much closer than the node spacing. Using first-order time-stepping we simulate, eg, 25 ellipses per unit cell to 3-digit accuracy on a desktop in 1 hour per shear time. Our examples show equilibration at long times, force chains, and two types of blow-ups (jamming) whose power laws match lubrication theory asymptotics.

Read the full article here.