Stochastic Block Models
Abstract
The stochastic block model (SBM) is a probabilistic model for community structure in networks. Typically, only the adjacency matrix is used to perform SBM parameter inference. In this paper, we consider circumstances in which nodes have an associated vector of continuous attributes that are also used to learn the node-to-community assignments and corresponding SBM parameters. Our model assumes that the attributes associated with the nodes in a network’s community can be described by a common multivariate Gaussian model. In this augmented, attributed SBM, the objective is to simultaneously learn the SBM connectivity probabilities with the multivariate Gaussian parameters describing each community. While there are recent examples in the literature that combine connectivity and attribute information to inform community detection, our model is the first augmented stochastic block model to handle multiple continuous attributes. This provides the flexibility in biological data to, for example, augment connectivity information with continuous measurements from multiple experimental modalities. Because the lack of labeled network data often makes community detection results difficult to validate, we highlight the usefulness of our model for two network prediction tasks: link prediction and collaborative filtering. As a result of fitting this attributed stochastic block model, one can predict the attribute vector or connectivity patterns for a new node in the event of the complementary source of information (connectivity or attributes, respectively). We also highlight two biological examples where the attributed stochastic block model provides satisfactory performance in the link prediction and collaborative filtering tasks.
Stanley, N., Bonacci, T., Kwitt, R. et al. Stochastic block models with multiple continuous attributes. Appl Netw Sci 4, 54 (2019). https://doi.org/10.1007/s41109-019-0170-z
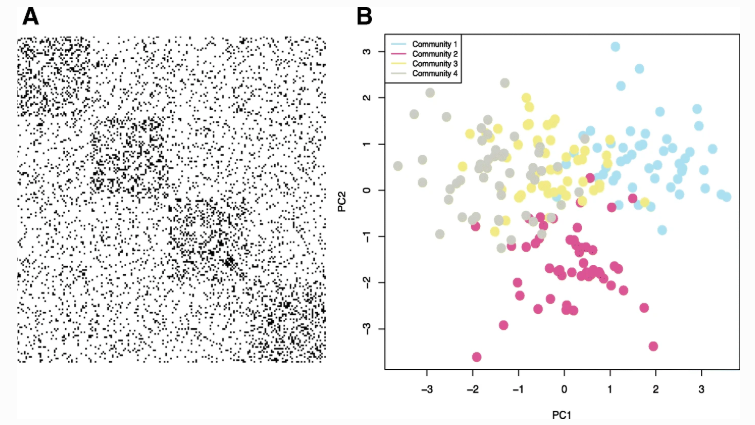
Synthetic Example. We generated a synthetic network with N=200 nodes, K=4 communities and an 8-dimensional multivariate Gaussian for each community. a. A visualization of the adjacency matrix for this network where a black dot indicates an edge. We observe that there is an assortative block structure (blocks on the diagonal), but there are also many edges between communities making the true community structure using only connectivity harder to detect. b. We performed PCA on the N×p attribute array and plotted each of the N nodes in two dimensions. Points are colored by their true community assignments, z. Clustering the nodes according to only connectivity, only attributes, and with the attributed SBM, we quantified the partition accuracy with normalized mutual information, yielding NMI(z,{zconnectivity,zattributes,zattribute sbm})={0.65,0.68,0.83}

